Google Web Mercator: a mixed coordinate system
the First of October 2014, the us National Geospatial-Intelligence Agency (NGA) has published report, which contained criticism of the coordinate system of the Web Mercator used in the web mapping services. The document was accompanied by a detailed explanation of the problem and recommendations for partners NGA. The document received a great response, but not all articles based on this report, very accurate and literate presentation. This applies, for example, articles on the website of the GIS Association, which, because of gross errors in terminology, can be considered illiterate. Because this coordinate system the developers of web services face more often, I think it makes sense to understand the problem.
what is it?
For a start, a couple definitions, without which some of the details may not be clear. It is important to understand that Web Mercator is the coordinate system, not only the projection, although its name is similar to many well-known Mercator projection. It is this terminological discrepancy misleads readers of the article on the website of the GIS Association. The difference between the projection and the coordinate system is that the projection is just the way the complex shape of model shape of the Earth flattened into a plane, while the coordinate system also includes a mathematical definition of the model (ellipsoid or spheroid), approximating the complex shape of the Earth.

In this illustration, marked with red that only applies to the mechanism of projection (in this case cylindrical). The coordinate system includes everything that is pictured here.
In turn, this is the most approximating model to the surface (dotted area in the figure above, where the coordinates λ,φ) and the source of the problem, about which more will be discussed.
History
I can't say for certain, who first and when all this came to mind. But, to my knowledge, the first major project to use the Web Mercator coordinate system, was Google Maps, and it happened in 2005. Developers had then the task to simplify the calculations necessary to work with cartographic data, and most obvious, thing to do is to use the coordinate system of the sphere instead of the ellipsoid. Interestingly, Sam Gerard Mercator, probably, proceeded from the same geometric representations, creating your way of projecting maps onto the plane, because only Newton, who lived somewhat later, proposed a hypothesis that the Earth because the centrifugal force has the form of ellipsoid of revolution, and not a ball. Thus, the developers at Google, in a sense, back to the sixteenth century.
Criticism of this approach in professional circles sounds not for the first time. Since 2005, the organisation European Petroleum Survey Group (EPSG) dealing with standardization in the field of coordinate systems and is the holder of the register IDs codes EPSG refused to assign the system to Web Mercator has its own official code, citing its deliberate geometric imperfection. Because in the Internet you can find references to this system through informal codes: EPSG:900913, EPSG:102113, and others. However, in 2008 this organization had to give up and give a code, as the popularity of the system grew, and it had clearly indicate not to produce an even greater anarchy. The first attempt to give a definition of the system was not entirely successful, but in the end she was given an official SRID EPSG:3857.
Algebra
Since the projection is the subject of study mathematics, I start with formulas and then give them a graphic illustration. Strictly speaking, do not even have to be proficient in trigonometry to understand the difference between the implementation of systems of coordinates based on the Mercator projection, the sphere in one case and an ellipsoid in the other. Formulas differ markedly in appearance.
x=a×λ,
y=a×ln[tan(π/4+φ/2)×((1-e×sinφ)/(1+e×sinφ))^(e/2)]
where:
x and y rectangular coordinates
λ is the longitude on the ellipsoid, in radians.
φ is the latitude on the ellipsoid, in radians,
a — the value of the major semiaxis of the ellipsoid,
e — the value of the eccentricity of the ellipsoid (the ratio of the major and minor semi-axes).
If instead of the ellipsoid used is sphere, as it is in the Web Mercator coordinate system, it becomes significantly easier as the formula for the ordinate (Y-axis) degenerates, giving the following:
x=a×λ,
y=a×ln[tan(π/4+φ/2)]
Agree, looks much simpler and shorter, and then sought developers Google. This makes it quite visibly reduce the number of mathematical operations when working with cartographic materials in both client and server applications.
Geometry and cartography
Even if you do not go into the formula, simple illustrations show good understanding of the problem. Let me explain first that the principle of the Mercator projection consists in the fact that any point on the surface of the ellipsoid or spheroid is projected onto a cylinder, inside which the ellipsoid is placed so that their vertical axes coincide, and the surface or touched by one line (most common case), or intersect both. (See illustration above). Further, a conventional projection rays emerge from the center of the ellipsoid intersect the surface at point P into the surface of the cylinder at point P', and where tolerated, a corresponding point on the surface of the Earth. It is easy to visualize that if the real surface of the Earth in this first projected not quite close to her the form of an ellipsoid, and an idealized sphere, the projection on the cylinder points of the sphere, the same source point earth's surface will be at a different distance from the equator along the vertical axis than in the case of the ellipsoid.
I'll try to illustrate "the scale of the disaster". Take archive NASA EOSDIS a satellite image in natural colors of the Central Federal district of Russia, made with a camera MODIS Aqua with a resolution of 250 meters per pixel 21 September 2014 (this day — because it was clear it would look better) — this will be our background.
Further, the query in Overpass Turbo unload from the database of the OpenStreetMap administrative boundaries of the Moscow region in the GeoJSON format. Query code:
the
Now, using Global Mapper, transform data borders the Moscow region from a geographic projection to the Mercator projection of the WGS84 ellipsoid. And then, to simulate the situation when the coordinate system is identified incorrectly, copy the resulting data and manually change the definition of the coordinate system to Web Mercator. In reality, rather a possible reverse situation: the data in Web Mercator can be taken for the data to WGS84/Mercator (it is more than possible because Web Mercator is still a lot of names, some of which is "WGS84"), however, from our simulation, it will differ only in the direction of the shift. The resulting data will load in Global Mapper, place them over a grid with increments of 100 kilometers and see what happens.
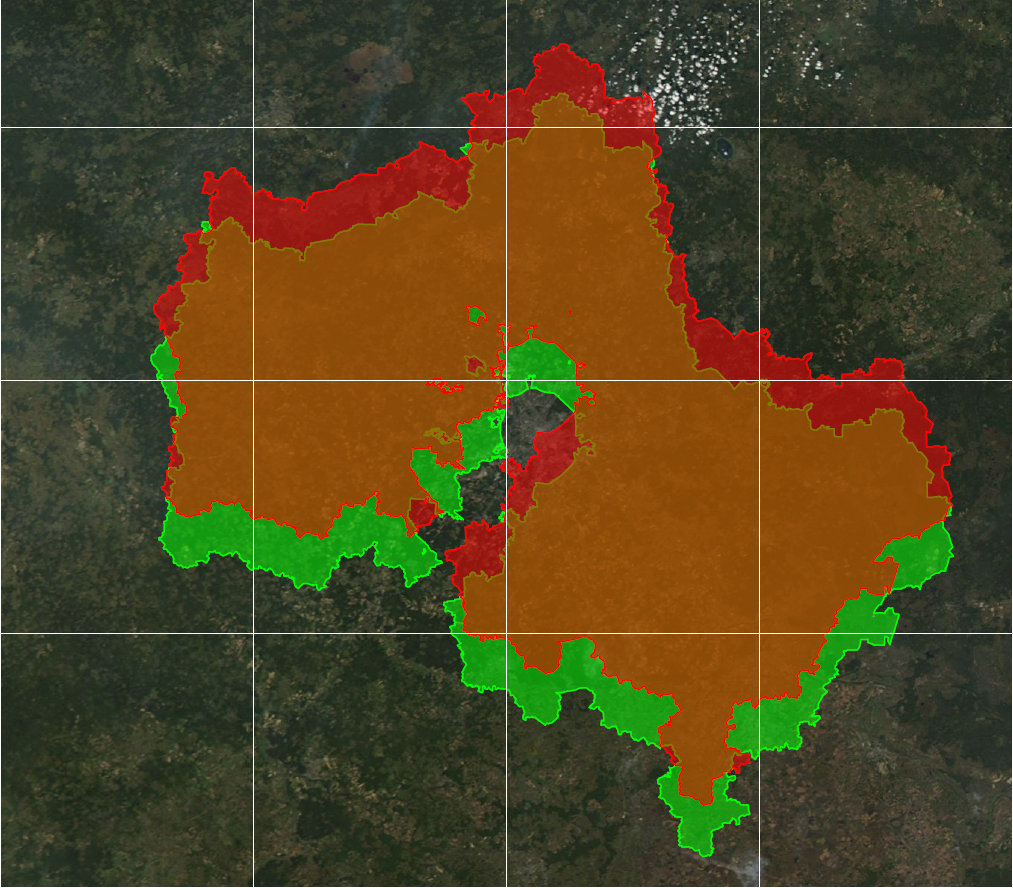
The green outline on the map is where you need it, and the red — shifted. The magnitude of this shift is 19.6 kilometers. This does not mean that this error exists in all map services that use this coordinate system, not at all. But it will manifest if you take this system and try to combine with other data without the correct account. In this case, it will apply the wrong reverse conversion to geographical coordinates, which will result in an error.
Navigation
Some map projections have special properties that are critical for solving navigation tasks. The Mercator projection is one of them, because it is widely used for marine and aeronautical charts. This is possible thanks to this geometric property of this projection as a conformal. In this case, it means that the shape of the object is large enough this map is maintained as the stored values of angles between the lines. For navigation this means that looking at the map, it is possible to calculate the direction of the required point with respect to the Meridian (the direction to true North), and moving in this direction on a magnetic compass or at a constant angle to the line on the North star to be in the right place. This path is called "loxodrome" and is the shortest route between two points on the Earth's surface and modern navigation devices make it possible to calculate the path for "autodrome" — is really the shortest line, but Mercator did not refuse, because the map made it, gives you the ability in an emergency to use the navigation tools instead of relying on GPS and other electronics.
And here is the Web Mercator coordinate system turns out to be false. Although it is based on the Mercator projection, but using a sphere with a constant radius, as the ultimate simplification of the model of the Earth's surface, depriving the properties of conformity. This means that moving with a constant course angle measured on a map will not be able to get to the desired point due to distortions of the angles in this coordinate system. It would seem that this is not so important for web services because they no one in their right mind would pave the way in an emergency. However, a variety of web services is large, and to ensure that someone from the developers will not want to assume any direction in this projection — it is impossible. In calculations in this projection error can be very hard to accumulate. Plus, now very popular tools like SAS.Planet that siphons data from web services, and nobody can predict what's next with these data will make the user.
The extent of the problem in this case is also quite easy to measure. Take the same picture for the background, the same data on the situation of the administrative border of Moscow region. Now we need three lines of orthodrome (shortest path taking into account the curvature of the Earth) and two loxodrome built in systems Mercator/WGS84 and Web Mercator. To build these lines will be between the southernmost point in Serebryanoprudskiy district of the region, near the village with the amusing name of Mochily and the most Northern in the Taldom district.
Build orthodromy. Now measure its length (it happened a little less than three hundred seven kilometers), and the initial angle relative to the Meridian. Then — the most interesting. Periprocedural working space in the Mercator projection and construct of the same initial reference line in this projection line by setting the measured angle and a length of 307 kilometers, not looking where she gets the other end. Repeat the same but in the Web Mercator coordinate system. Two loxodrome ready. For clarity, another find on orthodrome Central point, dividing it in half and placing the marker. Periprocedural workspace in WGS84 UTM 37N, to achieve minimum distortion of angles, proportions and other properties of the map.
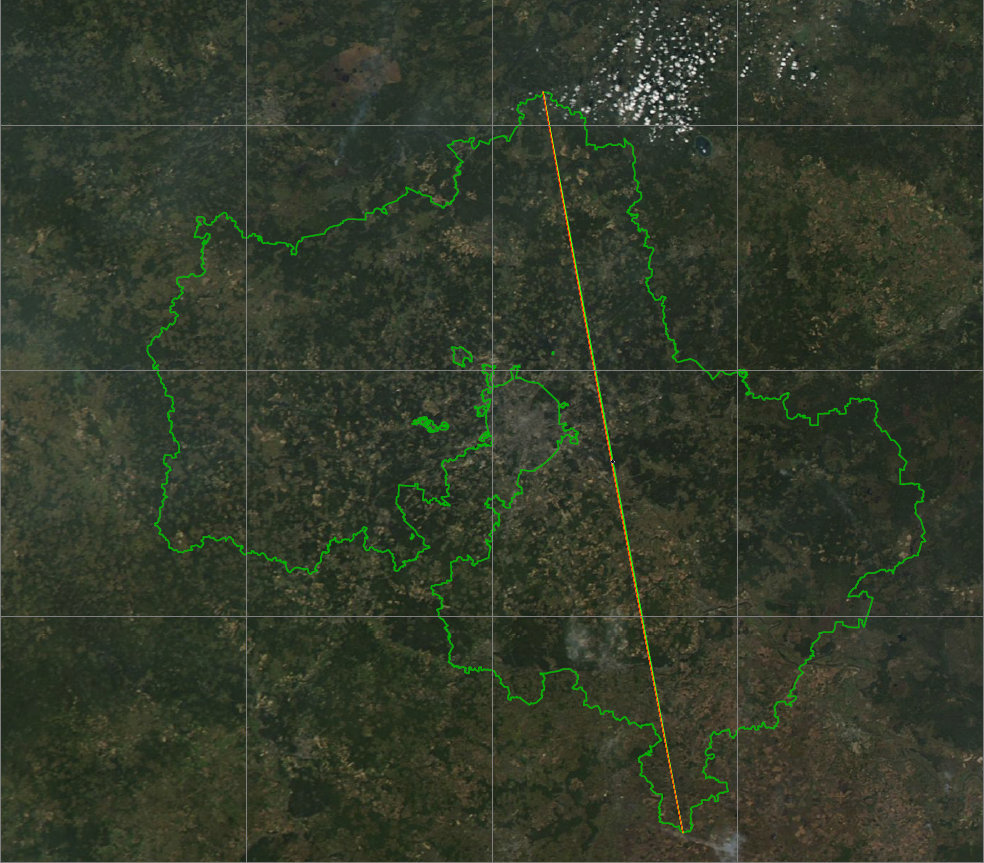
In this scale, almost nothing is impossible to sort out all the lines almost merge. But look closely at the center of the lines, including the pre-grid with a step of 100 meters.
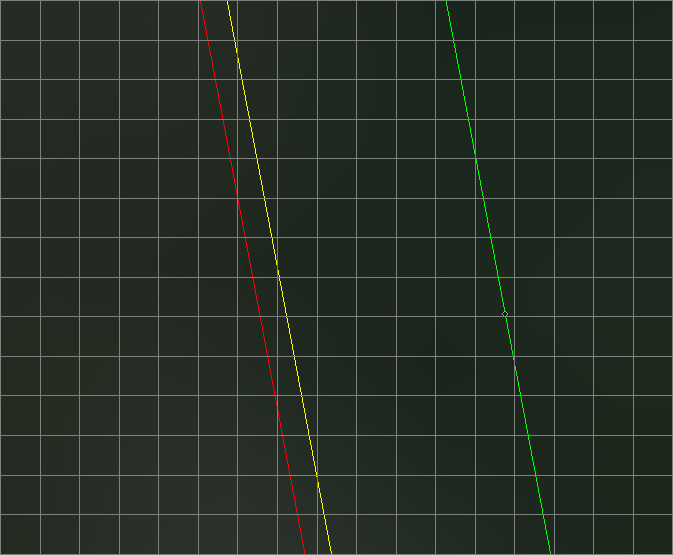
Green line with black dot on the map is orthodrome. Yellow — the rhumb line, which was built in the Mercator/WGS84, red — the rhumb line in Web Mercator. As expected, loxodrome left orthodromy because they are not the shortest distances and relatively straightforward orthodromy are arcs. Thoroughly gone more than 500 metres. But where are they leading us?

Yellow rhumb line, built in the Mercator projection of the WGS84 ellipsoid, describing the correct arc, "magically" returned to the desired point. This means that in this projection it is possible to get to the desired point, knowing the initial heading angle and moving all the time from this angle to the direction of the geographical North. And with the red it didn't work out — she missed more than one hundred and fifty meters. One hundred and fifty to three hundred thousand meters of the road. Four hundredths of a percent. It is a lot or a little? It is enough to consider its conformal and do not use for calculations where this is important.
the Names, appearance, passwords
The problem with the definition that uses the Web Mercator coordinate system — not invented. Because of her, shall we say, "anarchist" of the past she has so many names that it is just impossible to enumerate. However, I will try to demonstrate how much everything is terrible, listing only some of the famous names and codes of this coordinate system:
So this system looks at the format PROJ.4:
Here we should pay attention to equal values of the size parameters of the semiaxes of the ellipsoid a and b. Their equality and the means to use the scope. If it's "fair" of the Mercator projection of the WGS84 ellipsoid, she's EPSG:3395, in the format of PROJ.4 it is defined like this:
Another unpleasant situation is the existence of the definition of that coordinate system in the Well-known Text (WKT) in which the definition in WKT is almost identical to the definition for "fair" coordinate system using the WGS84 ellipsoid, that is, there is the string
the Logic of the situation
I'm not here trying to prove that the Web Mercator coordinate system will not do. Good, of course. And exactly the same output (except for matters where it is important that the military standards of the USA) can be found in the NGA report. It is important to understand the difference between coordinate systems and their capabilities. It is important to understand that Web Mercator is used almost everywhere: Google, OpenStreetMap, Bing, Yahoo and countless other services. She also laid out in the format Slippy Map Tiles, which stores a tiled raster data sources. It is so popular that not all who use it, think about how exactly it works. And to think sometimes it is worth it, especially if the planned service must perform functions that are more complex than a simple display of pictures with a map.
Some interesting facts instead of a conclusion
The NGA, the report which began a new round of this story, before the advent of such services as NASA World Wind, Google Maps, Yandex.Maps and others, was the only one available to any source of satellite imagery is relatively high resolution (10 meters per pixel, black-and-white image) on the territory of Russia, which was a free download through the service NIMA Raster Roam (NGA then still was called NIMA — National Imagery and Mapping Agency). These pictures were part of a reconnaissance program carried out by satellites since the fifties, trapped in the program of declassification in 1995.
Yandex.The card does not use the Web Mercator coordinate system, it uses a fair Mercator projection ellipsoid WGS84, EPSG:3395. What is the reason initially unknown to me, but it would be very interesting to hear the comments of the staff Yandex, here, on habré, are present in considerable quantity.
Local map services in the Scandinavian countries often don't use the Mercator projection at all, preferring the coordinate system adopted in these countries, for example, the Norwegian public service Norge i Bilder uses three projection zones UTM datum EUREF89. This is because in the Northern latitudes, the Mercator projection gives a too strong deformation of the scale.
Article based on information from habrahabr.ru
what is it?
For a start, a couple definitions, without which some of the details may not be clear. It is important to understand that Web Mercator is the coordinate system, not only the projection, although its name is similar to many well-known Mercator projection. It is this terminological discrepancy misleads readers of the article on the website of the GIS Association. The difference between the projection and the coordinate system is that the projection is just the way the complex shape of model shape of the Earth flattened into a plane, while the coordinate system also includes a mathematical definition of the model (ellipsoid or spheroid), approximating the complex shape of the Earth.

In this illustration, marked with red that only applies to the mechanism of projection (in this case cylindrical). The coordinate system includes everything that is pictured here.
In turn, this is the most approximating model to the surface (dotted area in the figure above, where the coordinates λ,φ) and the source of the problem, about which more will be discussed.
History
I can't say for certain, who first and when all this came to mind. But, to my knowledge, the first major project to use the Web Mercator coordinate system, was Google Maps, and it happened in 2005. Developers had then the task to simplify the calculations necessary to work with cartographic data, and most obvious, thing to do is to use the coordinate system of the sphere instead of the ellipsoid. Interestingly, Sam Gerard Mercator, probably, proceeded from the same geometric representations, creating your way of projecting maps onto the plane, because only Newton, who lived somewhat later, proposed a hypothesis that the Earth because the centrifugal force has the form of ellipsoid of revolution, and not a ball. Thus, the developers at Google, in a sense, back to the sixteenth century.
Criticism of this approach in professional circles sounds not for the first time. Since 2005, the organisation European Petroleum Survey Group (EPSG) dealing with standardization in the field of coordinate systems and is the holder of the register IDs codes EPSG refused to assign the system to Web Mercator has its own official code, citing its deliberate geometric imperfection. Because in the Internet you can find references to this system through informal codes: EPSG:900913, EPSG:102113, and others. However, in 2008 this organization had to give up and give a code, as the popularity of the system grew, and it had clearly indicate not to produce an even greater anarchy. The first attempt to give a definition of the system was not entirely successful, but in the end she was given an official SRID EPSG:3857.
Algebra
Since the projection is the subject of study mathematics, I start with formulas and then give them a graphic illustration. Strictly speaking, do not even have to be proficient in trigonometry to understand the difference between the implementation of systems of coordinates based on the Mercator projection, the sphere in one case and an ellipsoid in the other. Formulas differ markedly in appearance.
x=a×λ,
y=a×ln[tan(π/4+φ/2)×((1-e×sinφ)/(1+e×sinφ))^(e/2)]
where:
x and y rectangular coordinates
λ is the longitude on the ellipsoid, in radians.
φ is the latitude on the ellipsoid, in radians,
a — the value of the major semiaxis of the ellipsoid,
e — the value of the eccentricity of the ellipsoid (the ratio of the major and minor semi-axes).
If instead of the ellipsoid used is sphere, as it is in the Web Mercator coordinate system, it becomes significantly easier as the formula for the ordinate (Y-axis) degenerates, giving the following:
x=a×λ,
y=a×ln[tan(π/4+φ/2)]
Agree, looks much simpler and shorter, and then sought developers Google. This makes it quite visibly reduce the number of mathematical operations when working with cartographic materials in both client and server applications.
Geometry and cartography
Even if you do not go into the formula, simple illustrations show good understanding of the problem. Let me explain first that the principle of the Mercator projection consists in the fact that any point on the surface of the ellipsoid or spheroid is projected onto a cylinder, inside which the ellipsoid is placed so that their vertical axes coincide, and the surface or touched by one line (most common case), or intersect both. (See illustration above). Further, a conventional projection rays emerge from the center of the ellipsoid intersect the surface at point P into the surface of the cylinder at point P', and where tolerated, a corresponding point on the surface of the Earth. It is easy to visualize that if the real surface of the Earth in this first projected not quite close to her the form of an ellipsoid, and an idealized sphere, the projection on the cylinder points of the sphere, the same source point earth's surface will be at a different distance from the equator along the vertical axis than in the case of the ellipsoid.
I'll try to illustrate "the scale of the disaster". Take archive NASA EOSDIS a satellite image in natural colors of the Central Federal district of Russia, made with a camera MODIS Aqua with a resolution of 250 meters per pixel 21 September 2014 (this day — because it was clear it would look better) — this will be our background.
Further, the query in Overpass Turbo unload from the database of the OpenStreetMap administrative boundaries of the Moscow region in the GeoJSON format. Query code:
the
<osm-script output="json" timeout="25">
<union>
<query type="relation">
<has-kv k="name" v="Moscow oblast"/>
<has-kv k="boundary" v="administrative"/>
<bbox-query {{bbox}}/>
</query>
</union>
<print mode="body"/>
<recurse type="down"/>
<print mode="skeleton" order="quadtile"/>
</osm-script>
Now, using Global Mapper, transform data borders the Moscow region from a geographic projection to the Mercator projection of the WGS84 ellipsoid. And then, to simulate the situation when the coordinate system is identified incorrectly, copy the resulting data and manually change the definition of the coordinate system to Web Mercator. In reality, rather a possible reverse situation: the data in Web Mercator can be taken for the data to WGS84/Mercator (it is more than possible because Web Mercator is still a lot of names, some of which is "WGS84"), however, from our simulation, it will differ only in the direction of the shift. The resulting data will load in Global Mapper, place them over a grid with increments of 100 kilometers and see what happens.

The green outline on the map is where you need it, and the red — shifted. The magnitude of this shift is 19.6 kilometers. This does not mean that this error exists in all map services that use this coordinate system, not at all. But it will manifest if you take this system and try to combine with other data without the correct account. In this case, it will apply the wrong reverse conversion to geographical coordinates, which will result in an error.
Navigation
Some map projections have special properties that are critical for solving navigation tasks. The Mercator projection is one of them, because it is widely used for marine and aeronautical charts. This is possible thanks to this geometric property of this projection as a conformal. In this case, it means that the shape of the object is large enough this map is maintained as the stored values of angles between the lines. For navigation this means that looking at the map, it is possible to calculate the direction of the required point with respect to the Meridian (the direction to true North), and moving in this direction on a magnetic compass or at a constant angle to the line on the North star to be in the right place. This path is called "loxodrome" and is the shortest route between two points on the Earth's surface and modern navigation devices make it possible to calculate the path for "autodrome" — is really the shortest line, but Mercator did not refuse, because the map made it, gives you the ability in an emergency to use the navigation tools instead of relying on GPS and other electronics.
And here is the Web Mercator coordinate system turns out to be false. Although it is based on the Mercator projection, but using a sphere with a constant radius, as the ultimate simplification of the model of the Earth's surface, depriving the properties of conformity. This means that moving with a constant course angle measured on a map will not be able to get to the desired point due to distortions of the angles in this coordinate system. It would seem that this is not so important for web services because they no one in their right mind would pave the way in an emergency. However, a variety of web services is large, and to ensure that someone from the developers will not want to assume any direction in this projection — it is impossible. In calculations in this projection error can be very hard to accumulate. Plus, now very popular tools like SAS.Planet that siphons data from web services, and nobody can predict what's next with these data will make the user.
The extent of the problem in this case is also quite easy to measure. Take the same picture for the background, the same data on the situation of the administrative border of Moscow region. Now we need three lines of orthodrome (shortest path taking into account the curvature of the Earth) and two loxodrome built in systems Mercator/WGS84 and Web Mercator. To build these lines will be between the southernmost point in Serebryanoprudskiy district of the region, near the village with the amusing name of Mochily and the most Northern in the Taldom district.
Build orthodromy. Now measure its length (it happened a little less than three hundred seven kilometers), and the initial angle relative to the Meridian. Then — the most interesting. Periprocedural working space in the Mercator projection and construct of the same initial reference line in this projection line by setting the measured angle and a length of 307 kilometers, not looking where she gets the other end. Repeat the same but in the Web Mercator coordinate system. Two loxodrome ready. For clarity, another find on orthodrome Central point, dividing it in half and placing the marker. Periprocedural workspace in WGS84 UTM 37N, to achieve minimum distortion of angles, proportions and other properties of the map.

In this scale, almost nothing is impossible to sort out all the lines almost merge. But look closely at the center of the lines, including the pre-grid with a step of 100 meters.

Green line with black dot on the map is orthodrome. Yellow — the rhumb line, which was built in the Mercator/WGS84, red — the rhumb line in Web Mercator. As expected, loxodrome left orthodromy because they are not the shortest distances and relatively straightforward orthodromy are arcs. Thoroughly gone more than 500 metres. But where are they leading us?

Yellow rhumb line, built in the Mercator projection of the WGS84 ellipsoid, describing the correct arc, "magically" returned to the desired point. This means that in this projection it is possible to get to the desired point, knowing the initial heading angle and moving all the time from this angle to the direction of the geographical North. And with the red it didn't work out — she missed more than one hundred and fifty meters. One hundred and fifty to three hundred thousand meters of the road. Four hundredths of a percent. It is a lot or a little? It is enough to consider its conformal and do not use for calculations where this is important.
the Names, appearance, passwords
The problem with the definition that uses the Web Mercator coordinate system — not invented. Because of her, shall we say, "anarchist" of the past she has so many names that it is just impossible to enumerate. However, I will try to demonstrate how much everything is terrible, listing only some of the famous names and codes of this coordinate system:
Web Mercator, Google Web Mercator, Spherical Mercator, WGS 84 Web Mercator, WGS 84/Pseudo-Mercator (despite the fact that "pseudo" there is just not a Mercator, WGS84), WGS84 Web Mercator (Auxiliary Sphere), Popular Visualisation CRS / Mercator WGS84 / Simple Mercator.
EPSG:900913, EPSG:3785, EPSG:3857, EPSG:102113, ESPG:102100, EPSG:41001.
So this system looks at the format PROJ.4:
+proj=merc +lon_0=0 +k=1 +x_0=0 +y_0=0 +a=6378137 +b=6378137 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs Here we should pay attention to equal values of the size parameters of the semiaxes of the ellipsoid a and b. Their equality and the means to use the scope. If it's "fair" of the Mercator projection of the WGS84 ellipsoid, she's EPSG:3395, in the format of PROJ.4 it is defined like this:
+proj=merc +lon_0=0 +k=1 +x_0=0 +y_0=0 +ellps=WGS84 +datum=WGS84 +units=m +no_defsAnother unpleasant situation is the existence of the definition of that coordinate system in the Well-known Text (WKT) in which the definition in WKT is almost identical to the definition for "fair" coordinate system using the WGS84 ellipsoid, that is, there is the string
SPHEROID["WGS 84",6378137,298.257223563,AUTHORITY["EPSG","7030"], but then either found is overriding this string Declaration PARAMETER["semi_minor",6378137.0], or do a hell of EXTENSION["PROJ4","+proj=merc +a=6378137 +b=6378137 +lat_ts=0.0 +lon_0=0.0 +x_0=0.0 +y_0=0 +k=1.0 +units=m +nadgrids=@null +wktext +no_defs"],AUTHORITY["EPSG","3857"]. The problem with such definitions (coming in a PRJ file with some data) is that no one guarantees you that the software that you these data will discover, will understand what he should do in such a contradictory definition as the first option. And the introduction of a definition string in the format PROJ.4 contrary to everything that is written in WKT is actually a subtle perversion, as it is unknown who actually supports this. It turns out that in the best case, the program will give an error about unreadable content defining a coordinate system, and at worst — will try to interpret this jumble, ignoring the incomprehensible, and that will cause the data to Web Mercator will be read as data in "fair" WGS84/Mercator.the Logic of the situation
I'm not here trying to prove that the Web Mercator coordinate system will not do. Good, of course. And exactly the same output (except for matters where it is important that the military standards of the USA) can be found in the NGA report. It is important to understand the difference between coordinate systems and their capabilities. It is important to understand that Web Mercator is used almost everywhere: Google, OpenStreetMap, Bing, Yahoo and countless other services. She also laid out in the format Slippy Map Tiles, which stores a tiled raster data sources. It is so popular that not all who use it, think about how exactly it works. And to think sometimes it is worth it, especially if the planned service must perform functions that are more complex than a simple display of pictures with a map.
Some interesting facts instead of a conclusion
The NGA, the report which began a new round of this story, before the advent of such services as NASA World Wind, Google Maps, Yandex.Maps and others, was the only one available to any source of satellite imagery is relatively high resolution (10 meters per pixel, black-and-white image) on the territory of Russia, which was a free download through the service NIMA Raster Roam (NGA then still was called NIMA — National Imagery and Mapping Agency). These pictures were part of a reconnaissance program carried out by satellites since the fifties, trapped in the program of declassification in 1995.
Yandex.The card does not use the Web Mercator coordinate system, it uses a fair Mercator projection ellipsoid WGS84, EPSG:3395. What is the reason initially unknown to me, but it would be very interesting to hear the comments of the staff Yandex, here, on habré, are present in considerable quantity.
Local map services in the Scandinavian countries often don't use the Mercator projection at all, preferring the coordinate system adopted in these countries, for example, the Norwegian public service Norge i Bilder uses three projection zones UTM datum EUREF89. This is because in the Northern latitudes, the Mercator projection gives a too strong deformation of the scale.
Комментарии
Отправить комментарий